백준9694 - 무엇을 아느냐가 아니라 (다익스트라) Python 본문
반응형
https://www.acmicpc.net/problem/9694
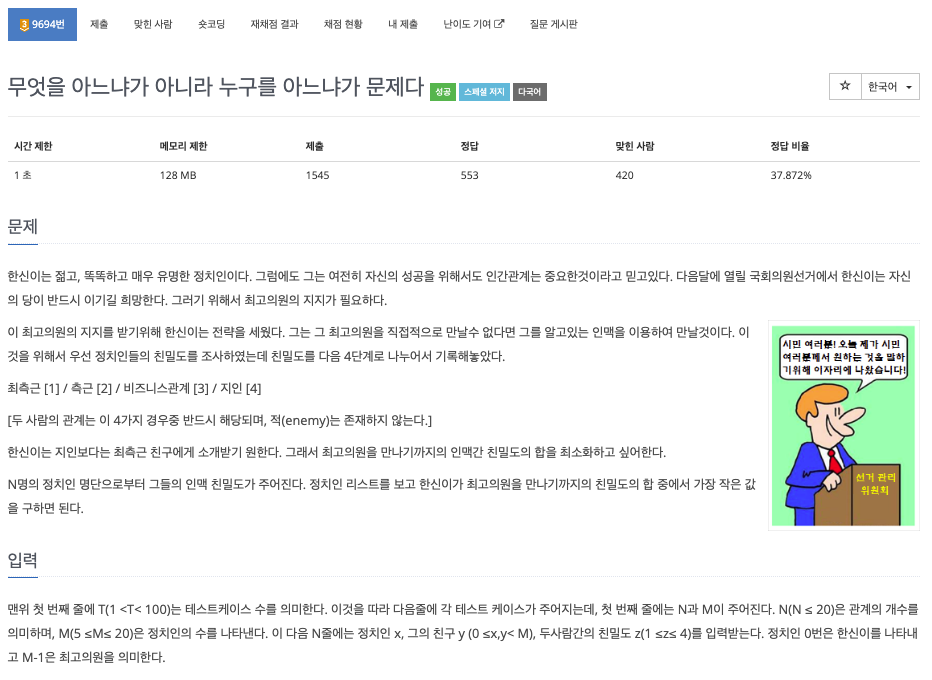
문제는 거리를 가중치하여 한 정점(0)에서부터 특정한 정점(N-1)까지의 최단 거리를 찾고,
최단 거리가 존재하는 경우 최단 거리까지 경유하는 정점하는 정점들을 반환, 없는 경우 -1을 반환하는 문제다.
문제에서 나와있듯, 한 정점에서 특정한 정점까지의 최단 거리이기 때문에 다익스트라 알고리즘으로 접근했고,
다익스트라 알고리즘이 실행되는 과정에서 각 정점들의 방문 기록을 남겼다.
입력값으로 주어진 하나의 테스트 케이스가 처리되는 과정을 담은 소스 코드는 다음과 같다.
(다익스트라 알고리즘에 관한 내용은 종종 다뤘기에 해당 포스팅에서는 생략하고 아래 링크로 대체한다.)
2023.11.14 - [개발/algorithm] - 백준1916 - 최소 비용 구하기 (다익스트라) Python
def act(index, arr) :
_,n = arr.pop(0)
graph = [[] for _ in range(n)]
# 각 노드별 기록을 담을 리스트
path = [[] for _ in range(n)]
for s,e,w in arr :
# 친구관계이므로 양방향 그래프로 설정
graph[s].append((w,e))
graph[e].append((w,s))
_txt = dijkstra(graph, path)
return f'Case #{index+1}: {_txt}'
def dijkstra (graph, path) :
dp = [float('inf') for _ in range(len(graph))]
dp[0] = 0
pq = []
# 문제에서 제시된 첫 시작점이 0이므로 path = [[0]]
path[0] = [0]
heapq.heappush(pq, (0, 0))
while pq :
wei, node = heapq.heappop(pq)
if wei > dp[node] : continue
for n_wei, n_node in graph[node] :
total_wei = wei + n_wei
if dp[n_node] > total_wei :
dp[n_node] = total_wei
# 다음 방문 기록 = 이전 방문 기록에 다음 정점을 추가한 기록
path[n_node] = path[node] + [n_node]
heapq.heappush(pq, (total_wei, n_node))
return ' '.join(map(str, path[-1])) if path[-1] else '-1'즉, 기존 익숙한 다익스트라 알고리즘에서 path라는 리스트를 활용해 방문 기록들을 저장하는 로직이 추가되었다.
전체 소스 코드
import sys
data_temp = sys.stdin if sys.platform == 'linux' else open('입력.txt', 'r')
input_data = data_temp.read().splitlines()
import heapq
def solution (data) :
int(data.pop(0))
arr = [list(map(int, x.split())) for x in data]
# 입력값에 따른 테스트케이스 분류
tc = []
j = 0
for _ in range(len(arr)) :
if j > len(arr) - 1 : break
a,_ = arr[j]
tc.append(arr[j:j+a+1])
j += (a + 1)
result = list(map(lambda x : act(x[0],x[1]), enumerate(tc)))
print('\n'.join(result))
def act(index, arr) :
_,n = arr.pop(0)
graph = [[] for _ in range(n)]
path = [[] for _ in range(n)]
for s,e,w in arr :
graph[s].append((w,e))
graph[e].append((w,s))
_txt = dijkstra(graph, path)
return f'Case #{index+1}: {_txt}'
def dijkstra (graph, path) :
dp = [float('inf') for _ in range(len(graph))]
dp[0] = 0
pq = []
path[0] = [0]
heapq.heappush(pq, (0, 0))
while pq :
wei, node = heapq.heappop(pq)
if wei > dp[node] : continue
for n_wei, n_node in graph[node] :
total_wei = wei + n_wei
if dp[n_node] > total_wei :
dp[n_node] = total_wei
path[n_node] = path[node] + [n_node]
heapq.heappush(pq, (total_wei, n_node))
return ' '.join(map(str, path[-1])) if path[-1] else '-1'
solution(input_data)반응형
'개발 > algorithm' 카테고리의 다른 글
| 백준16946 - 벽 부수고 이동하기 4 (DFS) Python (2) | 2023.11.26 |
|---|---|
| 백준2468 - 안전 영역 (DFS) Python (1) | 2023.11.25 |
| 백준11404 - 플로이드 (플로이드 워셸) Python (0) | 2023.11.23 |
| 프로그래머스 - Lv.3 순위 (플로이드-워셸) Python (0) | 2023.11.22 |
| 백준14235 - 크리스마스 선물 (힙) Python (1) | 2023.11.21 |
Comments




