백준1916 - 최소 비용 구하기 (다익스트라) Python 본문
https://www.acmicpc.net/problem/1916
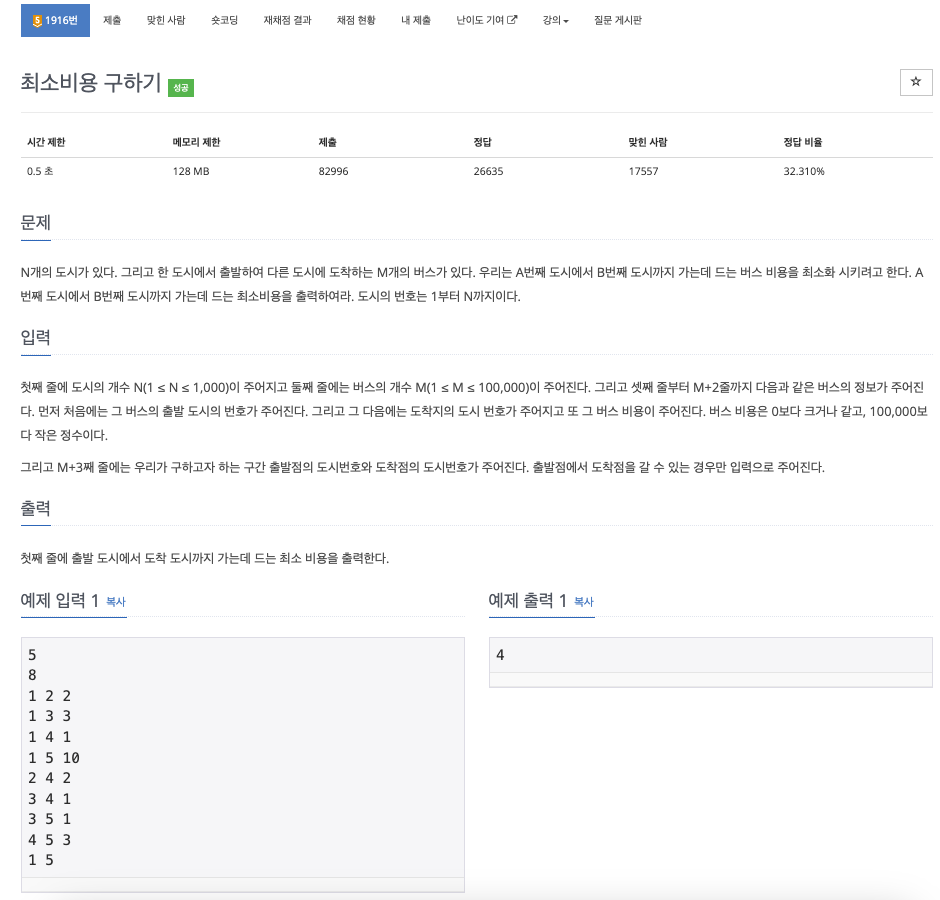
해당 문제는 N개의 정점과, 그 도시들을 잇는 M개의 간선과 가중치가 주어질 때,
특정 두 정점의 최소 가중치(간선 | 경로의 비용 | 거리)를 구하는 문제다.
언뜻 너비우선탐색(BFS)와 비슷한 개념으로 풀이하면 될까 싶지만, 해당 문제는 다익스트라라는 개념으로 접근해야 한다.
(개념에 대한 학습은 구글과 함께 했다. ^_^)
먼저 너비우선탐색 알고리즘과 다익스트라 알고리즘에 대해 비교하자면 다음과 같다.
- 너비우선탐색 알고리즘은 가중치가 없는 그래프에서 최단 경로를 찾는 것에 적합.
- 다익스트라 알고리즘은 가중치가 있는 그래프에서 최단 경로를 찾는 것에 적합.
- 너비우선탐색 알고리즘은 일반적으로 큐(Queue)로 구현.
- 다익스트라 알고리즘은 일반적으로 힙(Heap)로 구현. (힙 == 우선순위 큐)
다익스트라 알고리즘의 구현 과정
1. 모든 정점의 최단 거리를 무한대로 초기화.
2. 출발 정점을 선택하고 출발 정점의 최단 거리를 0으로 초기화.
3. 아직 방문하지 않은 정점 중 최단 거리가 가장 적은 정점을 선택. (첫 정점은 출발 정점)
4. 해당 정점과 인접한 정점의 최단 거리를 갱신.
5. 모든 정점을 방문할 때까지 3번과 4번을 반복.
해당 문제에 대한 풀이를 코드로 옮겨쓰면 다음과 같다.
import sys
data_temp = sys.stdin if sys.platform == 'linux' else open('입력.txt', 'r')
input_data = data_temp.read().splitlines()
import heapq
def solution (data) :
# 입력 데이터 정제
arr = list(map(lambda x : list(map(int, x.split())), data))
[N], _, [start,end] = arr.pop(0),arr.pop(0),arr.pop()
# 그래프 구현
graph = [[] for _ in range(N+1)]
# s,e,c 순서대로 출발 노드, 도착 노드, 가중치(비용) 의미
for s,e,c in arr :
graph[s].append((e,c))
# 다익스트라 함수에 인자 전달
result = dijkstra(graph, start, end)
print(result)
def dijkstra(graph, start, end) :
# 1. 모든 정점의 최단 거리를 무한대로 초기화
distances = [float('inf') for _ in range(len(graph))]
# 2. 출발 정점의 최단 거리를 0으로 초기화
distances[start] = 0
# 우선순위큐(힙) 초기화
queue = []
# 시작 정점을 우선순위큐에 대입
heapq.heappush(queue, (start, 0))
# 5. 최단 거리 갱신 반복
while queue :
# 3. 아직 방문하지 않은 정점 중 최단 정점이 가장 적은 정점 선택
cur_city, cur_cost = heapq.heappop(queue)
# 해당 정점의 가중치가 기존 가중치보다 크다면 스킵
if cur_cost > distances[cur_city] :
continue
# 4. 해당 정점과 인접한 정점들의 최단 거리를 갱신
for (next_city, next_cost) in graph[cur_city] :
# 기존 가중치 합이 신규 가중치 합보다 크다면
# 기존 가중치를 신규 가중치로 갱신
sum_cost = cur_cost + next_cost
if distances[next_city] > sum_cost :
distances[next_city] = sum_cost
heapq.heappush(queue, (next_city, sum_cost))
return distances[end]
solution(input_data)
개인적으로 느끼기에 다익스트라 알고리즘은 그래프 이론 | 자료구조 | 다이나믹 프로그래밍에 대한 개념이 혼재되어 있어,
해당 개념들에 대한 이해가 미흡하면 다익스트라 알고리즘 자체를 이해하기 어려울 것 같다는 생각이 들었다.
따라서 해당 개념들에 대해 익숙하지 않다면, 따로 자신이 부족한 부분을 학습하기를 추천드린다.
'개발 > algorithm' 카테고리의 다른 글
| 백준1261 - 알고스팟 (다익스트라) Python (0) | 2023.11.16 |
|---|---|
| 프로그래머스 - lv.3 합승 택시요금 (다익스트라) Python (0) | 2023.11.15 |
| 백준12789 - 도키도키 간식드리미 (스택) Python (0) | 2023.11.13 |
| 백준1935 - 후위 표기식 2 (스택) Python (1) | 2023.11.12 |
| 백준15815 - 천재 수학자 성필 (스택) Python (0) | 2023.11.11 |



