프로그래머스 - lv.3 합승 택시요금 (다익스트라) Python 본문
반응형
https://school.programmers.co.kr/learn/courses/30/lessons/72413
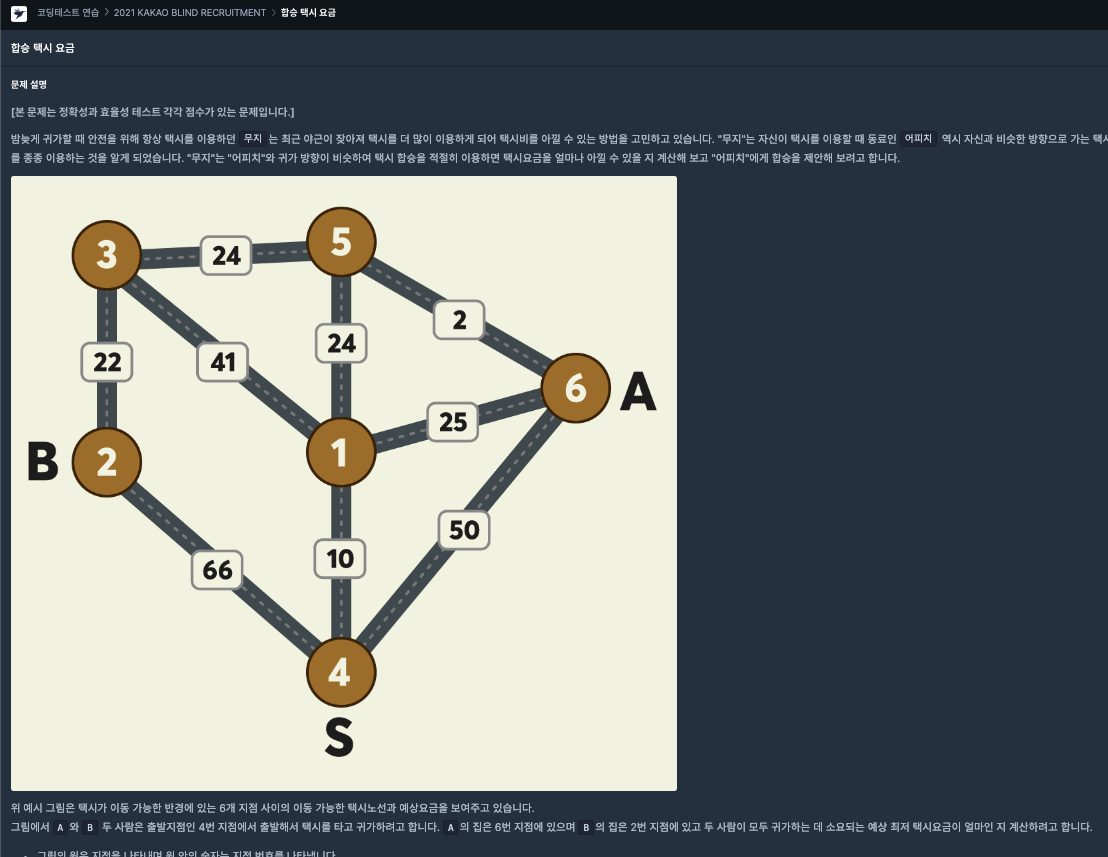
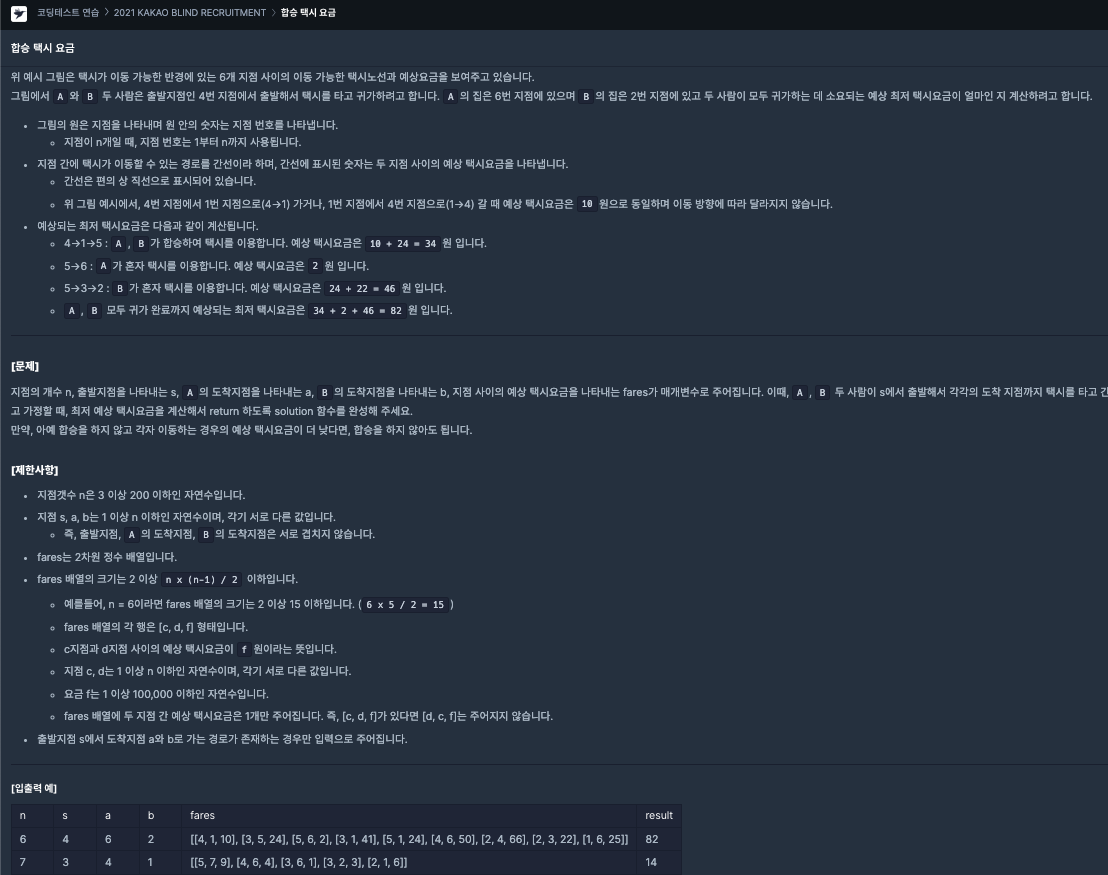
문제는 n개의 지점, 시작 지점 s, a의 도착 지점, b의 도착지점, [시작지점, 도착지점, 택시비]를 원소로 갖는 2차원 배열이 주어질 때,
a,b가 s에서 출발하여 각각 도착지점까지 택시를 타고 간다고 했을 때의 최저 예상금액을 구하는 문제다.
예전에 프로그래머스 문제들을 탐방하다가 보았던 문제인데, 다익스트라 개념을 알고나서 바로 도전했다.
문제에서 나올 수 있는 A,B가 택시를 탈 때 나오는 경우는 아래와 같이 세 가지로 나눌 수 있다.
# A->B 라면, A에서 B까지 가는 경우를 말한다.
1. A,B가 합승 없이 따로 목적지까지 가는 경우와 (X->A + X->B)
# 이때, 둘이 합승했을 경우의 비용이 제외되므로, 시작지점에서 경유지점까지의 비용 0
2. 시작점에서 A를 경유하여 B로 가는 경우(S->A(X) + A->B), B를 경유하여 A로 가는 경우(S->B + B->A)
# 만약, A를 경유한다면, 경유지점에서 A까지의 비용은 0
3. 일정 지점까지만 합승하고 특정 지점에서 따로가는 경우(S->X + X->A + X->B)따라서 다음과 같은 식의 수립이 가능하다.
시작점 S에서 경유지점 X까지의 비용 (S->X) + 경유지점 X에서 A까지의 비용 (X-> A) + 경유지점 X에서 B까지의 비용 (X -> B)
문제해결 과정은 다음과 같다.
먼저, 주어진 이차원 배열을 활용하여 그래프를 구현했다.
def solution(n,s,a,b,fares):
graph = [[] for _ in range(n + 1)]
for [_from,_to,w] in fares :
graph[_from].append((w,_to))
graph[_to].append((w,_from))
이후 다익스트라 알고리즘을 구현했다.
시작 노드를 매개변수로 할 때, 각 노드에 도달하기 위한 최소비용을 담은 배열을 반환하도록 했다.
def dijkstra(graph, start) :
dp = [float('inf') for _ in range(len(graph))]
dp[start] = 0
pq = []
heapq.heappush(pq, (0, start))
while pq :
cur_wei, cur_node = heapq.heappop(pq)
if cur_wei > dp[cur_node] : continue
for next_wei, next_node in graph[cur_node] :
total_wei = cur_wei + next_wei
if dp[next_node] > total_wei :
dp[next_node] = total_wei
heapq.heappush(pq, (total_wei, next_node))
return dp
이후 각 노드에 도달하기 위한 최소비용을 담은 배열을 한 곳에 담은 뒤
위에서 언급한 식을 활용하여 최솟값을 찾을 수 있도록 했다.
costs = [[]]
for i in range(n) :
costs.append(dijkstra(graph,i+1))
result = float('inf')
for i in range(n) :
result = min(result, costs[s][i+1] + costs[i+1][a] + costs[i+1][b])
전체 소스 코드
import heapq
def solution(n,s,a,b,fares):
graph = [[] for _ in range(n + 1)]
for [_from,_to,w] in fares :
graph[_from].append((w,_to))
graph[_to].append((w,_from))
costs = [[]]
for i in range(n) :
costs.append(dijkstra(graph,i+1))
result = float('inf')
for i in range(n) :
result = min(result, costs[s][i+1] + costs[i+1][a] + costs[i+1][b])
return result
def dijkstra(graph, start) :
dp = [float('inf') for _ in range(len(graph))]
dp[start] = 0
pq = []
heapq.heappush(pq, (0, start))
while pq :
cur_wei, cur_node = heapq.heappop(pq)
if cur_wei > dp[cur_node] : continue
for next_wei, next_node in graph[cur_node] :
total_wei = cur_wei + next_wei
if dp[next_node] > total_wei :
dp[next_node] = total_wei
heapq.heappush(pq, (total_wei, next_node))
return dp반응형
'개발 > algorithm' 카테고리의 다른 글
| 백준15787 - 기차가 어둠을 헤치고 은하수를 (비트마스킹) Python (0) | 2023.11.18 |
|---|---|
| 백준1261 - 알고스팟 (다익스트라) Python (0) | 2023.11.16 |
| 백준1916 - 최소 비용 구하기 (다익스트라) Python (1) | 2023.11.14 |
| 백준12789 - 도키도키 간식드리미 (스택) Python (0) | 2023.11.13 |
| 백준1935 - 후위 표기식 2 (스택) Python (1) | 2023.11.12 |
Comments



