프로그래머스 - Lv.3 순위 (플로이드-워셸) Python 본문
https://school.programmers.co.kr/learn/courses/30/lessons/49191
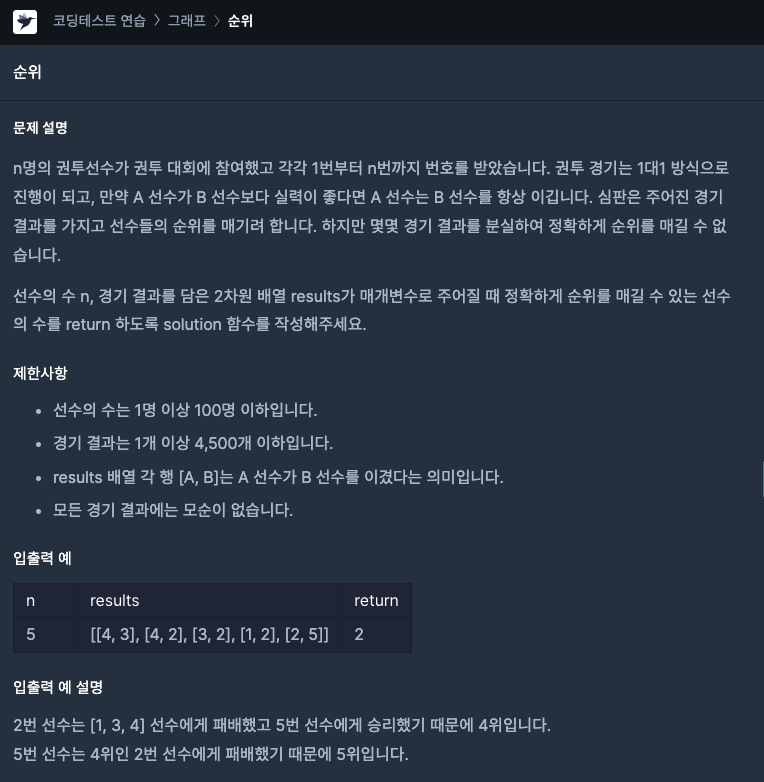
해당 문제는 선수의 수 n과 경기 결과를 담은 이차원 배열이 주어질 때, 정확하게 순위를 매길 수 있는 선수의 수를 리턴하는 문제다.
이때 선수 A,B,C가 있고, A가 B를 이기고, B가 C를 이겼다고 한다면, A가 C를 이긴다는 점을 주의깊게 보아야 한다.
이를 해결하기 위해선 먼저 경기 결과를 그래프로 구현한다.
이때, 모든 경로를 자신을 제외하고는 무한대로 설정했는데, 이는 아래 플로이드 워셸 동작 방식에서 설명한다.
def solution(n, results):
graph = [[float('inf')] * (n+1) for _ in range(n+1)]
for i in range(1,n+1) :
graph[i][i] = 0
for winner, loser in results :
graph[winner][loser] = 1
이후 모든 정점 쌍 사이의 최단 경로를 찾는 알고리즘인 플로이드-워셸 알고리즘으로 모든 정점을 탐색하며 승패자를 결정짓는 로직을 구현할 수 있다.
최단거리하면 떠오르는 다익스트라 알고리즘과는 다른데,
다익스트라 알고리즘은 한 지점에서 다른 특정 지점까지의 최단 거리를 구하는 방식이지만
플로이드-워셸 알고리즘은 모든 지점에서 다른 모든 지점까지의 최단 경로를 파악하는데 사용된다.
플로이드-워셸 알고리즘의 동작 방식은 다음과 같다.
- 그래프의 인접 행렬을 초기화하고, 인접하지 않은 정점 사이의 거리는 무한대로 표시하고 자기 자신으로 가는 거리는 0으로 표시.
- 모든 정점을 중간 정점으로 순회하며 경로를 개선하며, 중간 정점을 거쳐가는 경로가 더 짧은 경우 해당 경로로 거리 수정.
- 위 단계를 모든 정점을 중간 정점으로 순회하여 반복.
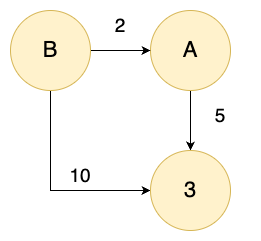
예를 들면, 위와 같은 그래프가 있다고 할 때, 플로이드-워셸 알고리즘은 중간 정점인 A부터 순회하며 경로를 개선한다.
정점 B에서 정점 C으로 가는 거리가 10인 경우, 정점 B 에서 정점 A로 가는 거리 + 정점 A에서 정점 C으로 가는 거리가 더 저렴하기 때문에
정점 B에서 정점 C로 가는 거리는 7로 수정된다.
여기서 플로이드-워셸의 점화식이 나오는데,
A를 중간 정점, B를 시작 정점, C를 도착 정점이라 할 때 아래와 같이 표현이 가능하다.
B에서 C까지의 거리 = (B에서 C까지의 거리, B에서 A까지의 거리 + A에서 C까지의 거리) 중 최솟값
따라서 해당 알고리즘을 활용하여 그래프를 최단 거리로 갱신한다.
for i in range(1, n+1) : # 중간정점
for j in range(1, n+1) : # 시작정점
for k in range(1, n+1) : # 도착정점
graph[j][k] = min(graph[j][k], graph[j][i] + graph[i][k])
이후 아래 로직으로 순위를 알 수 있는 선수를 파악할 수 있다.
result = 0
for i in range(1, n+1) :
count = 0
for j in range(1, n+1) :
# 두 간선 중 하나라도 무한대가 아니라면 연결되어 있는 관계를 의미
if graph[i][j] != float('inf') or graph[j][i] != float('inf') :
count += 1
if count == n :
result += 1
return result
전체 소스 코드
def solution(n, results):
graph = [[float('inf')] * (n+1) for _ in range(n+1)]
for i in range(1,n+1) :
graph[i][i] = 0
for winner, loser in results :
graph[winner][loser] = 1
for i in range(1, n+1) :
for j in range(1, n+1) :
for k in range(1, n+1) :
graph[j][k] = min(graph[j][k], graph[j][i] + graph[i][k])
result = 0
for i in range(1, n+1) :
count = 0
for j in range(1, n+1) :
if graph[i][j] != float('inf') or graph[j][i] != float('inf') :
count += 1
if count == n :
result += 1
return result
print(solution(5, [[4, 3], [4, 2], [3, 2], [1, 2], [2, 5]]))
'개발 > algorithm' 카테고리의 다른 글
| 백준9694 - 무엇을 아느냐가 아니라 (다익스트라) Python (1) | 2023.11.24 |
|---|---|
| 백준11404 - 플로이드 (플로이드 워셸) Python (0) | 2023.11.23 |
| 백준14235 - 크리스마스 선물 (힙) Python (1) | 2023.11.21 |
| 백준2234 - 성곽 (비트마스킹 & DFS) Python (1) | 2023.11.20 |
| 백준1194 - 달이 차오른다, 가자. (비트마스킹 & BFS) Python (1) | 2023.11.19 |



