프로그래머스 - Lv.2 타겟넘버 / 깊이 우선 탐색(DFS)와 너비 우선 탐색(BFS) 구현 방식 비교 본문
DFS, BFS는 모두 그래프를 탐색하는 알고리즘이다.
먼저 node란?
그래프 이론에서 주로 사용되는 용어로, 트리나 그래프 구조의 개별적인 요소를 의미한다.
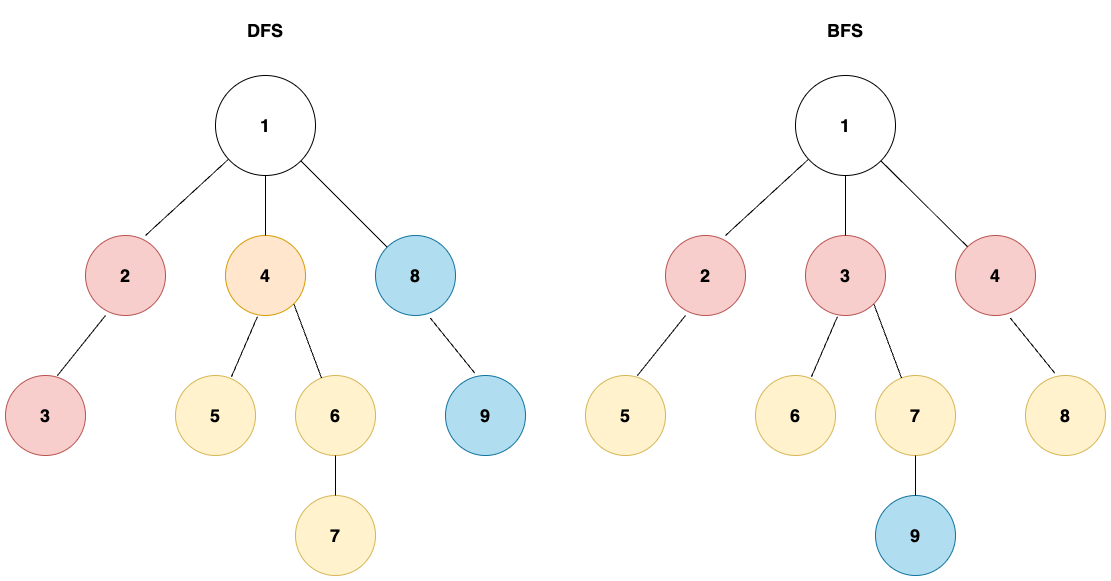
위 그림에서도 보여지는 것과 같이, DFS와 BFS의 차이점은 어떤 방식으로 다음 노드를 탐색하느냐에 따라 나뉜다. (색상으로 구분했다.)
DFS (깊이 우선 탐색)
DFS의 경우는 그 말마따나, 인접한 노드를 '깊이'있게 모두 탐색한 뒤에 다음 노드로 넘어가는 방식이다.
느리기는 하지만 간단하며, 모든 노드를 방문하고자 하는 경우에는 위 방법을 사용하며 스택 또는 재귀함수로 구현된다.
(DFS는 미로에서 100% 탈출하는 방법이라고 말하는 수법(손을 활용한 방식)과 비슷한 방법이라고도 볼 수 있는데,
궁극적으로 두 방법은 모든 경로를 파악하며 답을 도출하는 과정이라는 점에서 같은 맥락을 가진다.)
BFS (너비 우선 탐색)
BFS는 DFS와 반대로 가까운 노드를 먼저 탐색하며 나아가는 방식이다.
주로 두 노드 사이의 최단 경로를 찾고 싶을 때 이와 같은 방법을 선택하며, 큐를 사용하여 구현한다.
(그리고 이는 "인스타그램과 같은 SNS에서 자신의 지인과 연결된 사용자를 추천해주는 기능"과 같은 맥락을 가진다.)
두 알고리즘 모두 그래프 방식으로 모든 노드를 탐색한다는 점에서 같은 시간복잡도를 가진다고 볼 수 있지만,
상황에 따라 적합한 탐색 방식을 선택하는 것이 좋아보인다.
예시문제
예시문제는 프로그래머스의 "타겟넘버"라는 문제를 가져왔다.

DFS 풀이 방식
function solution(numbers, target) {
let result = 0
function recursive(index, sum) {
if (index === numbers.length) {
if (sum === target) {
result++
}
} else {
recursive(index + 1, sum + numbers[index]) // ***
recursive(index + 1, sum - numbers[index])
}
}
recursive(0, 0)
return result
}
solution([1,1,1,1,1],3)해당 풀이는 재귀함수를 활용하여 풀이하였다.
2023.01.24 - [개발/algorithm] - algorithm - 재귀함수
먼저 풀이과정을 설명하기 전에 연산을 나타낸 그림을 보면 이해하기 편할 것 같다.

위와 같이 해당 로직은 한쪽 방향으로 노드가 한계에 닿을 때까지 이어진다. 여기서는 연산이 모두 이루어진 뒤 target값과 비교하게 되므로 (index === numbers.length)라는 조건으로 한계를 두었다.
풀이에 대해 설명하자면 recursive 함수에서 처음 맞닥뜨린 재귀 함수(***로 표시하였음)가 재귀적으로 실행됨으로써, DFS 탐색을 가능케 한다. 마치 미로찾기에서 막힌 길을 되돌아 나오는 것 같은 느낌이 들기도한다.
사실 재귀함수가 두번 반복되는 까닭에 처음 이해하는 과정이 힘들었지만, 구현 자체는 비교적 간단한 편이라는 생각이 든다.
BFS 풀이 방식
function solution(numbers, target) {
let result = 0
let queueIdx = 0
const queue = [{ index: 0, sum: 0 }]
while (queue.length > queueIdx) {
const { index, sum } = queue[queueIdx]
if (index === numbers.length) {
if (sum === target) result++
} else {
queue.push({ index: index + 1, sum: sum + numbers[index] })
queue.push({ index: index + 1, sum: sum - numbers[index] })
}
queueIdx++
}
return result
}
solution([1,1,1,1,1],3)
해당 문제는 queue의 기본적인 틀을 사용했다.
일반적으로 queue는 FIFO(First in first out) 의 먼저 들어온 것이 먼저 나온다는 개념을 가진 자료구조인데,
여기서 배열에서 "먼저 나오는 것"을 구현하려면 연산이 무거운 shift()를 사용해야 하기에 대신 queueIdx라는 인덱스 값을 따로 매겨 풀이를 진행했다.
풀이 방식은 다음과 같다.
먼저 배열로 구현된 queue에 초기값을 삽입한다. 이때, 각 연산이 노드의 끝에 도달했을 때의 값을 target과 비교하게 되므로
배열의 길이와 index(깊이)를 비교하기 위한 index값 / target 과 합계를 비교하기 위한 sum을 키값으로 하여 { index: 0, sum: 0 }
queue.push({ index: index + 1, sum: sum + numbers[index] })
queue.push({ index: index + 1, sum: sum - numbers[index] })이후 다음 로직은 문제에 따라, 각 node의 sum이 가진 값에 + / - 를 하며 뿌리를 내리며 이어진다.

연산과정은 그림으로 표현하면 다음과 같고 궁극적으로 index 가 문제에서 제시된 배열의 길이와 같은 5까지 이어지면,
조건문에서 target 과 sum이 같은 요소가 발견될 경우 result에 1씩 추가되는 식으로 구현하였다.
추가로 while문이 반복될 때마다 조건문을 사용하는 방식이 아니라 아래와 같이 연산 마지막에 filter를 활용하는 방식 또한 괜찮을 것 같다.
function solution(numbers, target) {
let queueIdx = 0
const queue = [{ index: 0, sum: 0 }]
while (queue.length > queueIdx) {
const { index, sum } = queue[queueIdx]
if(index === numbers.length) break
queue.push({ index: index + 1, sum: sum + numbers[index] })
queue.push({ index: index + 1, sum: sum - numbers[index] })
queueIdx++
}
return queue.filter((el)=> el.index === numbers.length)
.filter((el)=> el.sum === target)
.length
}'개발 > algorithm' 카테고리의 다른 글
| 프로그래머스 - Lv.2 가장 큰 정사각형 찾기 / 동적 계획법 (DP) (0) | 2023.06.04 |
|---|---|
| new Array와 Array.from의 차이점 (0) | 2023.06.02 |
| mySQL 쿼리문 coalece / date_format / order by, having (0) | 2023.05.16 |
| 프로그래머스 - 200문제 풀이 기념 (0) | 2023.03.12 |
| 프로그래머스 - Lv.2 N개의 최소공배수 (0) | 2023.02.26 |



